P so với NP (giải nhanh chóng so với kiểm chứng nhanh chóng) là bài toán mở quan trọng trong lý thuyết khoa học máy tính. Có thể mô tả một cách đơn giản như sau: Nếu một bài toán có lời giải có thể kiểm chứng được nhanh chóng, liệu có thể tìm lời giải đó nhanh chóng hay không?
Chẳng hạn như trò chơi Sudoku, dù rất khó nhưng kiểm tra lại rất dễ (chỉ cần cộng lại các hàng, cột và đường chéo), đó chính là vấn đề.
P so với NP được Stephen Cook đưa ra năm 1971 trong bài báo nổi tiếng "The complexity of theorem proving procedures", được nhiều người xem là bài toán quan trọng nhất trong ngành khoa học máy tính.
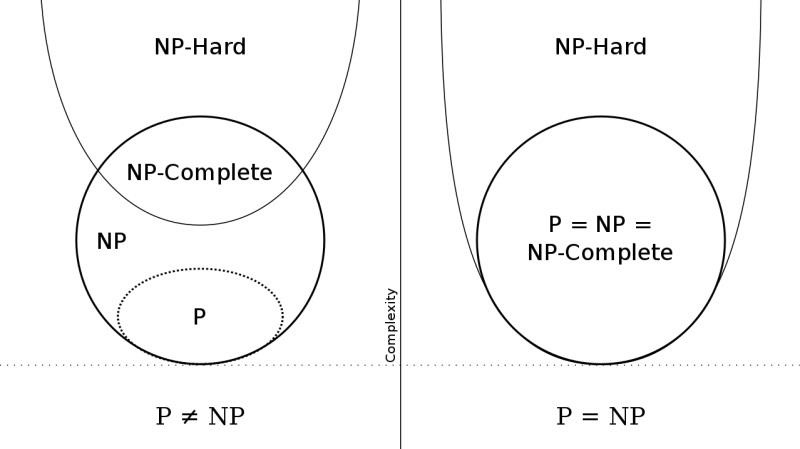 |
| Sơ đồ hiển thị các lớp vấn đề cần phải chứng minh để P = NP. Ảnh: Behnam Esfahbod. |
Đây cũng là một trong bảy bài toán thiên niên kỷ chọn bởi Viện Toán học Clay. Mỗi bài trong số bảy bài này có giải thưởng 1.000.000 USD cho lời giải đúng đầu tiên.
Lời giải bài toán P so với NP sẽ cho biết liệu tất cả các bài toán trong NP, như bài toán tổng tập hợp con, đều có thuật toán thực thi trong thời gian đa thức. Nếu P ≠ NP, thì có nhiều bài toán trong NP (chẳng hạn như các bài toán NP - đầy đủ) có lời giải có thể kiểm chứng được trong thời gian đa thức (khoảng thời gian hữu hạn nào đó có thể tính toán được) nhưng không thể tìm ra một lời giải như vậy trong thời gian đa thức.
Bài toán mở ra kho vàng
Nhà khoa học máy tính Scott Aaronson đã giải thích tại bài giảng trong Phòng thí nghiệm quốc gia Los Alamos ở New Mexico, chứng minh P = NP sẽ mở ra một số khả năng hấp dẫn.
Nếu ai đó giải quyết được bài toán P so với NP, điều đầu tiên họ làm là lấy 200 tỷ USD giá trị Bitcoin toàn cầu. Điều thứ hai là tiếp tục giải quyết tất cả bài toán thiên niên kỷ khác. Lúc này, họ sẽ đưa nhân loại “tiến hoá” thêm một bậc.
Để hiểu tại sao lại như vậy, cần biết máy tính là thiết bị giải quyết vấn đề, trong đó thông tin được trừu tượng thành mã có thể đọc được bằng thiết bị vật lý, dựa trên các nguyên tắc do Alan Turing đưa ra. Giải quyết vấn đề cần một số bước và khoảng thời gian nhất định, lượng thời gian cần thiết sẽ tăng lên khi vấn đề ngày càng lớn.
 |
| P so với NP được Stephen Cook đưa ra năm 1971 trong bài báo nổi tiếng "The complexity of theorem proving procedures". Ảnh: Kevin Van Paassen. |
Từ việc đơn giản nhân hai số đến các tác vụ phức tạp hơn như dùng trình duyệt Internet, máy tính về cơ bản đang cố giải quyết các phép toán nhân chia cộng trừ.
Khi một vấn đề phát triển phức tạp, lượng thời gian cần thiết để giải quyết tăng lên trong thời gian đa thức. Đa thức là một số có lũy thừa và hệ số (ví dụ như n luỹ thừa 2). Nếu một vấn đề có thể giải quyết được trong thời gian n mũ 2, khi tăng gấp đôi kích thước của vấn đề (2n), lượng thời gian cần thiết để giải quyết sẽ tăng lên bốn lần (2n luỹ thừa 2).
Như vậy, các tác vụ trong máy tính đều có thể tính được sau bao lâu thì máy tính giải quyết xong vấn đề được đưa ra.
Giải quyết và kiểm chứng
Có rất nhiều vấn đề trong đó người ta có thể kiểm tra một câu trả lời là đúng trong thời gian đa thức (tính được thời gian kiểm tra đáp án), nhưng quá trình để được câu trả lời đó có thể không là thời gian đa thức (tức là có thể tìm thấy lời giải hoặc không tìm thấy lời giải trong một khoảng thời gian nào đó, không thể xác định chính xác sau bao lâu thì tìm được lời giải).
Đây được gọi là các vấn đề NP “Nondeterministic Polynomial time” - vấn đề không xác định thời gian đa thức.
Sudoku là một vấn đề NP khó giải quyết, dễ kiểm tra. Ví dụ quan trọng khác là tách một số thành các số nguyên tố. Hiện phải mất một thời gian rất lâu, chậm hơn thời gian đa thức để tách các số rất lớn thành các số nguyên tố. Tuy nhiên, kiểm tra xem câu trả lời có đúng không chỉ đơn giản là nhân các số kết quả với nhau. Ý tưởng này là nền tảng của mã hóa hiện đại, dựa trên việc tạo các khóa bảo mật dễ xác minh nhưng khó bẻ khóa.
 |
| Nếu chứng minh được P=NP, bạn sẽ làm lủng đoạn toàn bộ hệ thống bảo mật thế giới chứ không riêng Bitcoin. Ảnh: Cryptoline News. |
Người ta từng nghĩ rằng máy tính lượng tử có thể giải quyết được các vấn đề NP khó nhất, được gọi là các vấn đề NP-đầy đủ. Nhưng không như kì vọng, máy tính lượng tử chỉ có thể giải quyết một số vấn đề P trong thời gian ngắn hơn (đa thức thấp hơn) hoặc chuyển một số vấn đề NP sang khái quát lượng tử của P, được gọi là BQP hoặc Thời gian đa thức lỗi Bounded-Error.
Do hiện tại người ta vẫn chưa chứng minh được P = NP, toàn bộ hệ thống mã hoá của chúng ta vẫn còn đảm bảo an ninh. Hacker phải mất nhiều thời gian để bẻ khoá hơn là thời gian tạo ra các khoá đó. Bitcoin cũng dựa trên nền tảng mã hoá này, do đó, nó vẫn còn là loại tiền tệ an toàn.
Nếu có thể tìm ra giải pháp hiệu quả cho những vấn đề NP-đầy đủ, bạn có thể tìm giải pháp hiệu quả cho tất cả các vấn đề NP. Điều này cho phép bạn giải quyết một loạt các vấn đề tối ưu hóa tương tự khác.
Nếu thành công trong việc chứng minh P bằng NP, bạn sẽ kiếm được ít nhất 1 triệu USD, thậm chí còn nhiều hơn thế nữa. Nếu không thành công cũng tốt, nó cho thấy các hệ thống mã hoá toàn cầu vẫn còn được đảm bảo an ninh.


