Có một nhóm người trên thế giới thực sự tin Trái Đất là phẳng. Họ cho rằng những tấm ảnh hành tinh chúng ta chụp từ vệ tinh đã được chính phủ dàn xếp nhằm thuyết phục mọi người Trái Đất hình cầu. Bằng chứng của họ là đường chân trời chẳng xuất hiện đường cong nào cả.
Điều thú vị là, ngay từ 2.000 năm trước, chẳng cần bất cứ vệ tinh nào, con người đã biết Trái Đất là một khối cầu.
Bởi vì Trái Đất phải có dạng tròn
Người Hy Lạp cho rằng Trái Đất dạng tròn trước cả khi họ có bằng chứng thuyết phục. Triết gia kiêm nhà toán học lỗi lạc Pythago là người đầu tiên đưa ra giả thuyết Trái Đất hình cầu những năm 500 TCN, dù rằng ông chỉ dựa trên góc nhìn thẩm mĩ của riêng mình: Hình cầu là dạng hoàn hảo nhất.
Một thế kỷ sau, nhà triết học Plato cũng đưa ra ý kiến tương tự, đồng thời khiến cho nhận định này trở nên phổ biến.
 |
| Ngay từ thời cổ đại, một số học giả đã tin tưởng Trái Đất có dạng hình cầu. Ảnh: Curiosity. |
Khi bắt đầu đi vào chứng minh Trái Đất hình tròn, Aristotle là triết gia người Hy Lạp tiên phong trong vấn đề này. Trong cuốn sách ''Trên thiên đàng'' (On the Heavens), viết vào năm 350 TCN, ông đã đưa ra một vài bằng chứng chứng minh Trái Đất hình cầu.
Ông chỉ ra rằng chúng ta có thể nhìn thấy bóng của Trái Đất trên Mặt Trăng trong các kì nguyệt thực. Nó luôn có dạng tròn bất kể Trái Đất ở vị trí nào trên vòng xoay của nó.
Trong luận điểm khác, ông thấy rằng vị trí các vì sao sẽ khác nhau khi chúng ta nhìn ở những nơi khác nhau trên Trái Đất. Những vì sao ở Ai Cập ko thể thấy được ở Cyprus cách đó 1.000 km.
 |
| Eratosthenes là một trong những người tiên phong trong việc dùng thực nghiệm để tính toán đường cong Trái Đất. Ảnh: Famous Mathematicians. |
"Điều đó chứng minh, Trái Đất không chỉ có dạng tròn mà ắt hẳn nó còn là một khối cầu với kích thước không lớn lắm. Nếu không, chỉ cần thay đổi địa điểm một chút thôi, không thể nhận ra sự khác biệt nhanh chóng và rõ ràng như vậy", ông viết.
Một học giả khác sau đó đã củng cố giả thuyết của Aristotle: Không chỉ chứng minh Trái Đất hình cầu, người này còn tính toán chu vi của nó chỉ bằng bóng đổ của một thanh que dưới ánh Mặt trời.
Người đàn ông và cây gậy
Eratosthenes là một trong những học giả nổi tiếng bật nhất vào thời của ông, nghiên cứu hầu hết lĩnh vực về khoa học. Năm 240 TCN, ông được bổ nhiệm làm thủ thư tại thư viện Alexandria - một trung tâm tài liệu vô cùng lớn, có thể ví như Google thời nay.
Một trong những tham vọng của ông là vẽ được bản đồ toàn thế giới. Để thực hiện nó, Eratosthenes biết rằng ông cần phải xác định kích thước của Trái Đất.
Ông từng nghe kể về câu chuyện một cái giếng tại thành phố Syene (nay là Aswan, Ai Cập) có những tính chất rất riêng biệt. Vào buổi trưa trong ngày hạ chí, ngay lúc Mặt trời trên đỉnh đầu, ánh sáng chiếu thẳng xuống đáy giếng mà không để lại bất kì cái bóng nào.
Để kiểm tra xem điều tương tự có xảy ra tại Alexandria hay không, Eratosthenes đặt một cây gậy thẳng đứng cũng vào ngày hạ chí lúc giữa trưa, nó để lại cái bóng với một góc 7,2 độ.
Eratosthenes nhận ra ông có thể làm một vài phép toán đơn giản để tính ra được chu vi của Trái Đất, điều ông cần biết là khoảng cách giữa Alexandria và Syene.
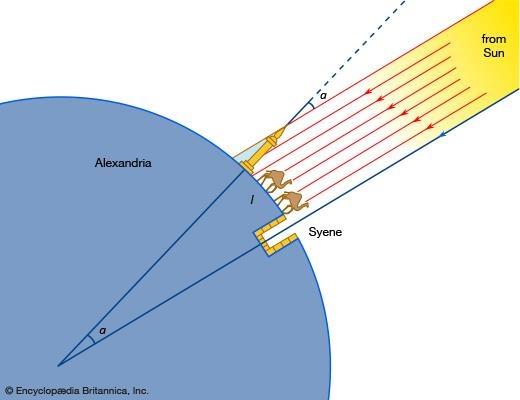 |
| Eratosthenes kết luận rằng khoảng cách từ Alexandria tới Syene bằng khoảng 7/360 chu vi Trái Đất. Ảnh: Schoolphysics. |
Cách thức đo lường khoảng cách lúc đó còn khá thô sơ, ông đã thuê những người đi rừng kì cựu, có thể biết chính xác số bước đi của họ, và đo khoảng cách giữa 2 thành phố là 5.000 stadia (khoảng 800-900km).
Với những số liệu này, Eratosthenes thực hiện phép tính nhanh. Khi Mặt trời vuông góc tại Syene và tạo góc 7,2 độ tại Alexandria, khoảng cách giữa hai thành phố vào khoảng 800-900km, vậy một vòng Trái Đất 360 độ sẽ ứng với 40.000km.
Dù giả định của ông bị lỗi, khoảng cách đưa ra cũng chưa chính xách, tính toán cuối cùng đưa ra chỉ lệch khoảng 75 km. Ngày nay, chúng ta biết rằng đường xích đạo Trái Đất là 40.075km, và kích thước sẽ nhỏ hơn một chút nếu đo theo đường kinh tuyến từ cực Bắc xuống cực Nam. Kết quả không tệ với một anh chàng cùng cây gậy của mình.