Tại sao những con số, những suy diễn có vẻ có lý lại dẫn chúng ta đến những nhận thức sai lầm. Đó là những gì tác giả Jordan Ellenberg muốn giải thích qua quyển sách Để không phạm sai lầm. Được sự đồng ý của Alphabooks - đơn vị giữ bản quyền - Zing trích đăng cuốn sách này.
Đến lúc này, cô bé tuổi teen đang nghe tôi nói sẽ dừng tôi lại và hỏi một câu hỏi khá hợp lý rằng: Thế toán học ở đâu? Wald là một nhà toán học, điều đó đúng và không thể phủ nhận rằng lời giải của ông cho bài toán lỗ đạn rất thông minh nhưng toán học liên quan gì tới việc đó? Chẳng thấy đẳng thức lượng giác nào, cũng chẳng có tích phân hay bất đẳng thức hay công thức nào.
Trước tiên, Wald quả thực có sử dụng các công thức. Tôi không đưa chúng vào câu chuyện, bởi vì đây chỉ mới là phần giới thiệu. Khi viết một cuốn sách giải thích việc sinh sản ở người cho các bé thiếu nhi, phần giới thiệu thường bỏ qua đoạn ướt át kể về việc làm cách nào em bé chui được vào trong bụng mẹ.
Thay vào đó, bạn thường bắt đầu câu chuyện như thế này: “Vạn vật trong tự nhiên đều biến đổi; cây cối rụng lá vào mùa đông để lại có thể nở hoa vào mùa xuân; con sâu bướm tầm thường chui vào kén để rồi lớn lên thành một chú bướm lộng lẫy. Em cũng là một phần của tự nhiên và do đó…”
Đó chính là phần giới thiệu của cuốn sách này.
Thế nhưng chúng ta đều là người lớn cả. Tạm gác lại sự lờ mờ này trong giây lát, một trang mẫu trong bản báo cáo thực sự của Wald trông như thế này. Hy vọng là nhìn không quá sốc:
 |
Dù vậy, ý tưởng thực sự đằng sau sự sáng suốt của Wald không cần đến bất kỳ phát biểu hình thức nào như ở trên. Chúng ta đã giải thích điều đó mà không sử dụng bất kỳ ký hiệu toán học nào. Cho nên câu hỏi của cô học trò của tôi vẫn có ý nghĩa. Vậy toán học là gì? Phải chăng đó chỉ là lẽ thường?
Đúng thế. Toán học là lẽ thường. Ở một mức độ cơ bản nào đó, điều này rất dễ hiểu.
Liệu bạn có thể giải thích cho ai đó tại sao bảy thứ cộng năm thứ cho ra cùng một kết quả với năm thứ cộng bảy thứ? Bạn không thể vì kiến thức này đã gắn liền với cách tư duy của chúng ta về sự kết hợp các thứ với nhau.
Các nhà toán học thích đặt tên cho hiện tượng mà chúng ta mô tả được bằng lẽ thường: thay vì nói “cái này cộng với cái kia cũng chính là cái kia cộng với cái này” thì họ nói “phép cộng có tính giao hoán”. Hoặc, vì thích các ký hiệu, họ sẽ viết:
Với mọi số a và b, ta có a + b = b + a.
Mặc dù công thức có vẻ nghiêm túc và cứng nhắc nhưng nó chỉ đang mô tả một kiến thức hiển nhiên mà đến một đứa trẻ cũng hiểu được theo bản năng.
Phép nhân lại là một câu chuyện hơi khác một chút. Công thức trông khá tương tự:
Với mọi số a và b, ta có a x b = b x a.
Trí óc chúng ta, khi xem xét biểu thức này, không nói “đương nhiên” ngay lập tức như trường hợp của phép cộng. Có phải “hiển nhiên” là hai bộ gồm sáu thứ có số lượng bằng sáu bộ gồm hai thứ?
Có thể không; nhưng nó có thể trở thành lẽ thường. Đây là ký ức toán học sớm nhất của tôi. Tôi đang nằm trên sàn trong ngôi nhà của bố mẹ, mà áp vào thảm lông, nhìn ngắm dàn âm thanh. Rất có thể khi đó tôi đang nghe mặt hai album Blue của nhóm Beatles. Có lẽ lúc đó tôi 6 tuổi.
Đây là những năm 70 nên dàn âm thanh được bọc một tấm gỗ ép có một dây hình chữ nhật các lỗ thoáng được đục ở mặt bên. Tám lỗ theo chiều ngang, sáu lỗ theo chiều từ trên xuống dưới. Tôi nằm đó, nhìn vào các lỗ ấy. Sáu hàng lỗ. Tám cột lỗ.
Bằng cách tập trung ánh nhìn qua lại, tôi có thể chuyển giữa việc nhìn các hàng và các cột. Sáu hàng, mỗi hàng tám lỗ. Tám cột, mỗi cột sáu lỗ.
Và rồi tôi nhận ra tám nhóm sáu cũng giống như sáu nhóm tám. Không phải vì đó là một quy tắc tôi được dạy, mà bởi vì nó không thể khác được. Số lượng lỗ trên tấm ốp là số lượng lỗ trên tấm ốp, bất kể ta có đếm chúng theo cách nào.
Chúng ta có xu hướng dạy toán học như là một dãy các quy tắc. Bạn học chúng theo thứ tự và phải tuân theo chúng, vì nếu không, bạn sẽ nhận điểm C-. Đó không phải là toán học. Toán học là việc nghiên cứu các sự việc xảy ra theo một cách nhất định nào đó bởi vì chúng không thể xảy ra theo cách nào khác.
Tuy nhiên, không phải mọi thứ trong toán học đều có thể được giải thích rõ ràng với trực giác của chúng ta như phép cộng và phép nhân.
Bạn không thể thực hiện phép tính vi phân và tích phân bằng lẽ thường. Nhưng phép tính vi phân và tích phân vẫn bắt nguồn từ lẽ thường - Newton lấy trực giác vật lý của chúng ta về các vật chuyển động trên đường thẳng, phát biểu nó ở dạng hình thức, và rồi xây dựng trên cấu trúc hình thức đó một mô tả toán học chung cho chuyển động.
Một khi nắm được lý thuyết của Newton, bạn có thể áp dụng nó để giải các bài toán vốn sẽ khiến bạn đau đầu nếu không có trợ giúp của các phương trình.
Theo cùng cách đó, chúng ta có các hệ thần kinh bẩm sinh để đánh giá khả năng của một kết quả không chắc chắn. Nhưng các hệ thống này khá yếu và không đáng tin cậy, đặc biệt đối với các sự kiện hiếm khi xảy ra. Đó là lúc chúng ta gia cố trực giác với các định lý và kỹ thuật chắc chắn, đúng chỗ, và dựa vào đó thành lập một lý thuyết xác suất toán học.
Ngôn ngữ chuyên môn mà các nhà toán học trao đổi với nhau là một công cụ tuyệt vời để truyền đạt các ý tưởng phức tạp một cách chính xác và nhanh chóng. Nhưng sự xa lạ của nó có thể khiến cho những người ngoại đạo có ấn tượng rằng lối tư duy đó hoàn toàn khác biệt với lối tư duy thông thường. Đó chính là chỗ sai lầm.
Toán học như một cơ quan nhân tạo chạy bằng năng lượng hạt nhân gắn vào hiểu biết thông thường của bạn, giúp gia tăng tầm với và sức mạnh của nó lên gấp bội. Bất kể sức mạnh của toán học, đôi khi là các ký hiệu và sự trừu tượng khó hiểu của nó, công việc tư duy thực sự của toán học chỉ hơi khác cách chúng ta tư duy về các vấn đề thực tiễn hơn.
Tôi thấy khá hữu ích khi ghi nhớ hình ảnh Người Sắt đấm thủng một lỗ trên một bức tường gạch. Một mặt, lực thực sự phá vỡ bức tường không phải nhờ cơ bắp của Tony Stark, mà là do một chuỗi cơ chế phụ đồng bộ tinh tế chạy bằng năng lượng từ một máy phát hạt beta nhỏ gọn.
Mặt khác, từ góc nhìn của Tony Stark, việc anh ta đang làm là đấm vào bức tường, hệt như cách anh ta vẫn làm nếu không có bộ áo giáp. Chỉ là sẽ khó hơn rất rất nhiều.
Để diễn đạt lại lời của Clausewitz: toán học là sự mở rộng của lẽ thường theo các cách khác.
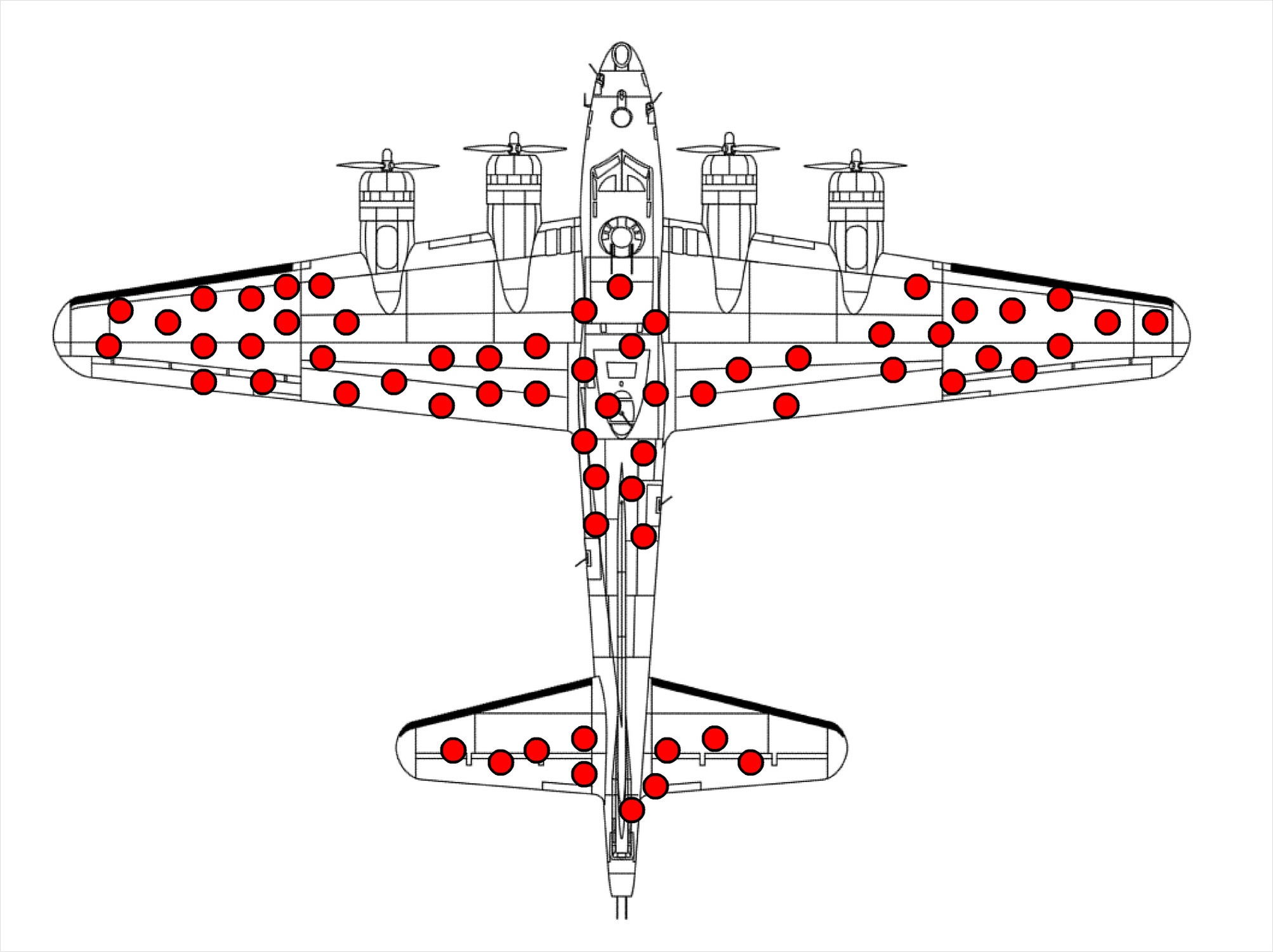
Nếu không có cấu trúc nghiêm ngặt của toán học, lẽ thường có thể đưa ta đi lạc lối. Đó là điều đã xảy ra với các sĩ quan muốn bọc giáp cho các bộ phận của máy bay vốn đã đủ chắc chắn.
Nhưng toán học hình thức nếu không có lẽ thường tức là không có sự tác động lẫn nhau giữa lập luận trừu tượng với trực giác của chúng ta về số lượng, thời gian, không gian, chuyển động, hành vi và sự không chắc chắn sẽ chỉ là một bài tập khô khan về việc tuân thủ quy tắc hay công việc kế toán.
Nói cách khác, toán học sẽ thực sự là thứ toán trong cách nghĩ của cô sinh viên học môn phép tính vi phân và tích phân hay bực bội kia. Đó là một nguy cơ thực sự.